二次関数で語れ

その１・二次関数グラフの極点・二次方程式の解

[関連JavaScriptはここをクリック][グラフが表示できないブラウザ用]

y=ax2+bx+cのグラフの極点を求めてみよう！

y=ax2+bx+cのグラフの極点って、要するに教科書では、a>0の場合は最小値、a<0の場合は最大値って書いてあるものですね？
そうです。まず、x2の係数aを出して括弧でくくります。
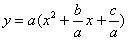
　　y=a{x2+(b/a)x+c/a}
xの係数b/aを2で割って無理やり(x+γ)2=x 2+2γx+γ2の形をつくります。
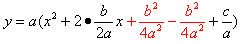
　　y=a{x^2+2･(b/2a)x+(b/2a)^2-(b/2a)^2+c/a}
x2+2γx+γ2の形の余りの部分を括弧の外に出して、最終的に二乗の形を作ります。
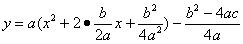
　　y=a{x^2+2･(b/2a)x+(b/2a)^2}-(b^2-4ac)/4a
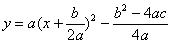　　y=a{x+(b/2a)x}^2-(b^2-4ac)/4a…①

さて、ここで、括弧の中身が実数（虚数や複素数ではない）のときは、
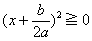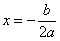　　{x+(b/2a)}^2≧0で、x=-b/2aのときが極小になります。
yの値はa>0のときはこの時最小（極小値）になるし、a<0のときは最大（極大値）になります。一々場合分けするのは面倒なので、極点って書くことにします。

で、極点の座標は、
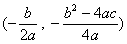
　　(-b/2a , -(b^2-4ac)/4a)

二次関数グラフの極点と、二次方程式の判別式・解との関係

この極点のy座標って、二次方程式 0=ax2+bx+c の判別式 D=b2-4ac を含みますね？
この二次方程式は、二次関数の式 y=ax2+bx+c がx軸と交わる点のx座標なので、当然関係が有るよね。グラフの形で考えてみると分かるけど、

a>0のときに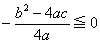-(b^2-4ac)/4a≦0ならx軸との交点がある。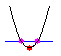

a<0のときに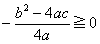-(b^2-4ac)/4a≧0ならx軸との交点がある。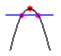
というわけで、結局、 b2-4ac≧0 が二次方程式の解が有る条件になる訳。
なるほど、もろに判別式と同じ意味になる訳ですね？？
ついでなので、中学校で習った解の公式についても復習しておきましょう。式①でy=0と置きます。
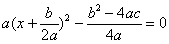
　　a{x+(b/2a)}^2-(b^2-4ac)/4a=0
式を変形して、
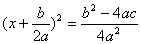
　　{x+(b/2a)}^2=(b^2-4ac)/4a^2
判別式が0以上のときは、左辺の2乗を外して、
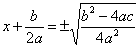
　　x+(b/2a)=(b^2-4ac)/4a^2
さらに、xについて解いて整理すると、
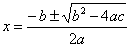
　　x={-b±√(b^2-4ac)}/2a
ということになります。

成るほど、極点の座標を求める式から解の公式が導けるわけですね？
うん、あんまり昔にやったことなので、すっかり忘れてたね（笑）。

いろいろな二次関数グラフを描いてみよう

せっかくグラフを描くJavaScriptを用意したので、少し遊んでみましょう。[ここをクリック]
  1. 判別式D=0となるようなグラフ、y=x2、y=x2+2x+1、y=x2+4x+4、y=x2+6x+9、y=x2+8x+16、などを描いてみてください。
    　　
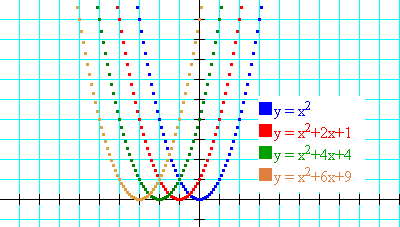
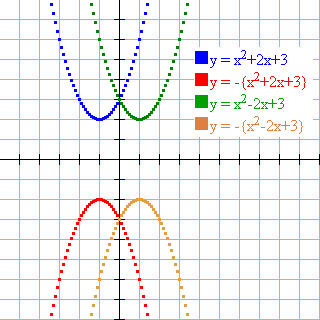
  2. 適当な二次関数、y=x2+2x-3などを描いてみて、次にyの係数を1から-1に変えてみてください。（x軸に対称な曲線が描けましたか？）
  3. 適当な二次関数、y=x2+2x-3などを描いてみて、次にx一乗の係数を2から-2に変えてみてください。（y軸に対称な曲線が描けましたか？）
  4. 適当な二次関数、y=x2+2x-3などを描いてみて、次にyの係数を1から-1に、同時にx一乗の係数を2から-2に変えてみてください。（原点に対称な曲線が描けましたか？）
  5. 適当な二次関数、y=x2+2x-3などを描いてみて、次にxにx=x-1を代入した式についてグラフを描いてみてください。(この場合はy=(x-1)2+2(x-1)-3=x2-4)(x方向に1移動したグラフができましたか？)
  6. 適当な二次関数、y=x2+2x-3などを描いてみて、次にxにy=y-1を代入した式についてグラフを描いてみてください。(この場合はy= x2+2x-2)(y方向に1移動したグラフができましたか？)
　
次へ　二次関数TOPへ

2008.07.05

[HOME][とまて週報TOP]